Cara Menghitung Volume Bola Kelas 6 SD/MI Kurikulum 2013
Latihan Soal
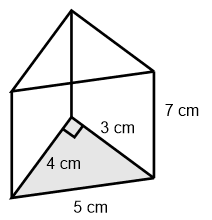
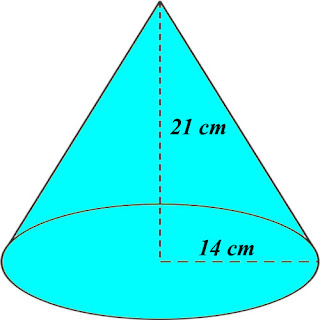
VOLUME BOLA
Bola adalah bangun ruang sehingga memiliki volume tertentu. Untuk menghitung volume sebuah bola, kita akan menggunakan rumus yang satu ini:
V =  x π x r3
x π x r3
Keterangan:
v = volume bola
r = panjang jari – jari bola
π = 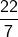 akan kita gunakan jika jari-jari (r) atau diameter (d) merupakan kelipatan 7 atau bisa dibagi 7
akan kita gunakan jika jari-jari (r) atau diameter (d) merupakan kelipatan 7 atau bisa dibagi 7
π = 3,14 akan kita gunakan jika jari-jari (r) atau diameter (d) bukan kelipatan 7 atau tidak bisa dibagi 7
Salah satu materi pelajaran bangun ruang di kelas 6 SD/MI adalah volume bola. Volume bola dapat di cara seperti contoh pada video di bawah ini!